Tensor derivatives and gradients

  The partial derivative of a tensor  is not generally itself a tensor although it is for a scalar : is a 0/1 tensor.

For a vector  , we have

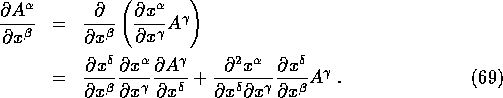
It follows that transforms like a 1/1 tensor only if the second term is zero, i.e.

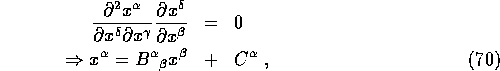
where and are constants. This is true for flat space with coordinates (ct,x,y,z) under the Poincaré transformations and in this case maybe interpreted as a 4D rotation matrix.

• Note however that it is not true for flat space with a general coordinate system or in the curved spacetime of General Relativity.

We can define the derivative of a general M/N tensor along a curve parameterized by the proper time as follows:

If the basis vectors and one- forms are the same everywhere then:

where

and is the tangent to the curve. Thus is also like a M/N tensor, written as

where means . We can then define a M/N+1 tensor :

This is the tensor gradient  [ remember the gradient of a scalar ].